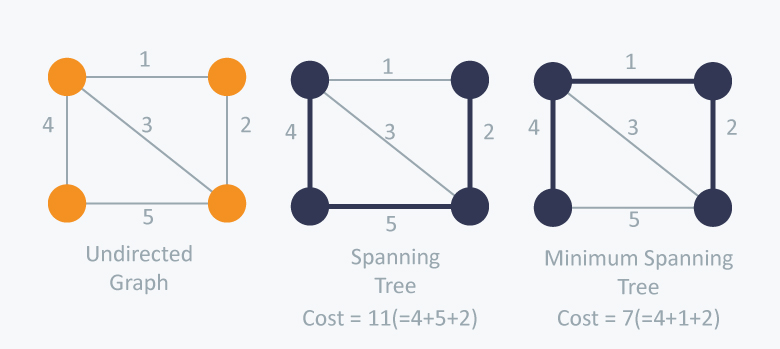
Spanning Tree는 그래프를 최소로 연결한 그래프입니다. 그렇기 때문에 N개 노드들이 있을때 모든 정점들이 연결 되어 있고 간선은 N-1개로 연결되어있습니다. 이때 사이클은 포함해서는 안됩니다.
최소 신장 트리는 Spanning Tree에서 사용된 간선들의 총 비용이 최소값을 가진 특수한 트리입니다.
- 최소 신장 트리가 최단 경로를 나타내지 않습니다. 최단 경로와 헷갈리면 안됩니다!!
- 예를 들어, N개의 정점에서 각 정점별 비용이 주어지고, 최소의 비용으로 모든 노드들간 서로 이동이 가능하도록 만드는 필요한 최소 비용을 구하라는 문제가 있을때 최소 신장 트리를 떠올려야 합니다.
최소 신장 트리를 만드는 방법은 두 가지 방법이 있습니다. 가장 많이 사용하는 방법으로 프림 알고리즘과 그 다음으로 크루스칼 알고리즘입니다. 프림 알고리즘은 정점을 추가하면서 트리를 확장하는 방법입니다. 크루스칼 알고리즘은 간선을 추가 하면서 최소 신장 트리를 만드는 방법입니다.
크루스칼 알고리즘
greedy 알고리즘을 기초로 그래프의 모든 정점을 최소 비용으로 연결하는 최적해를 구하는 방법입니다. 간선 선택을 기반으로 하고 있습니다.
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 정렬된 간선 리스트에서 순서대로 싸이클을 형성하지 않는 간선을 선택한다. 여기서 가장 작은 edge를 선택할때마다, 그 동안 연결한 노드들끼리 싸이클이 생기는지 확인해야 합니다. 이때 union-find 알고리즘을 사용합니다.
3. 해당 간선을 현재의 MST의 집합에 추가한다.
최소 스패닝 트리 구현 Python 코드 - [백준]1197번 : 최소 스패닝 트리
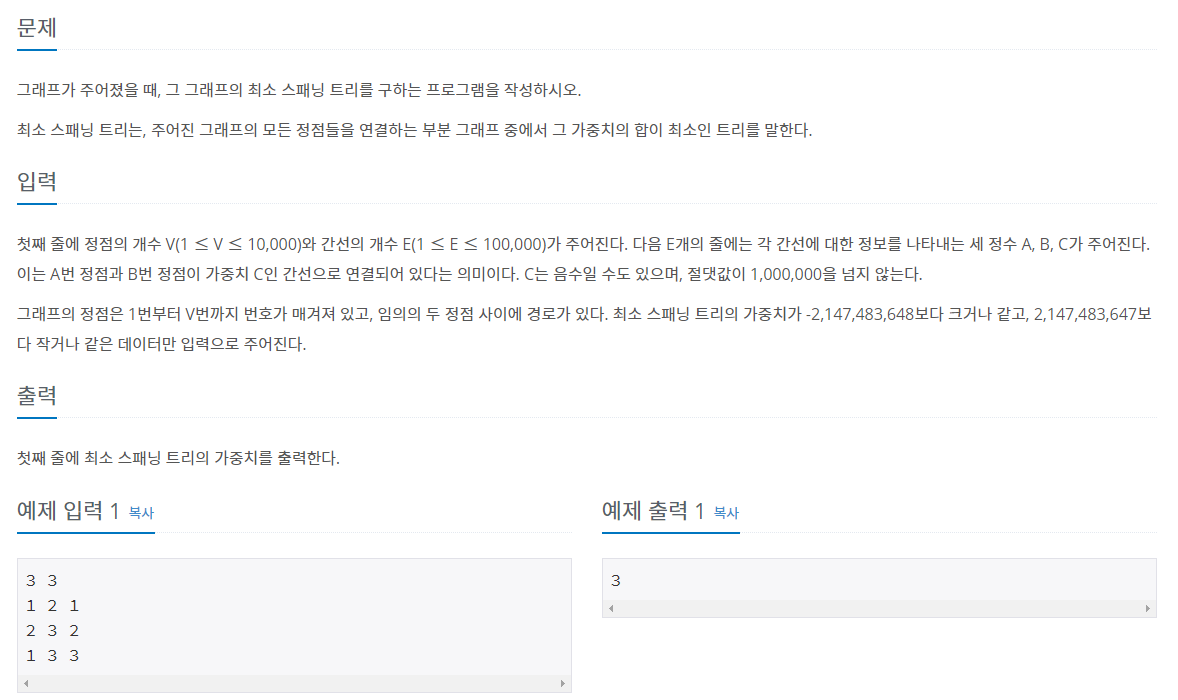
백준 최소 스패닝 트리 문제를 풀면서 크루스칼 알고리즘을 구현하겠습니다!
문제는 다음과 같습니다. (주석을 통해 설명했습니다. 위의 크루스칼 알고리즘 기본 로직과 주석 참고해주세요!!)
import sys
# v의 루트 노드 반환
def Find(v):
if(v == parent[v]):
return v
else:
p = Find(parent[v])
parent[v] = Find(parent[v])
return p
# u에는 u의 루트노드를 저장
# v에는 v의 루트노드를 저장
# 비교한다음 u에 v를 붙임 -> v의 루트노드를 x로 설정
def Union(u, v):
u = Find(u)
v = Find(v)
if(u!=v):
parent[v] = u
V, E = map(int, input().split())
graph = []
parent = [i for i in range(V+1)]
for _ in range(E):
u,v,cost = map(int, input().split())
graph.append([cost, u, v])
graph.sort(key=lambda x:x[0]) #간선(비용) 기준 오름차순 정렬
cnt = 0 # 모든 정점 연결되었는지 카운트
mst_weight = 0 # MST 가중치
for i in range(E):
weight = graph[i][0]
start = graph[i][1]
end = graph[i][2]
if Find(start) != Find(end):
Union(start,end)
mst_weight += weight
cnt += 1
if cnt == V-1:
break
print(mst_weight)유니온 파인드 Python 구현 코드 - [백준] 1717 집합의 표현
- 유니온 파인드는 서로소 집합 그리고 병합 찾기 집합이라고도 불리며 여러 서로소 집합의 정보를 저장하고 있는 자료구조를 뜻합니다.
- 백준 유니온 파인드 기본 문제를 통해 구현했습니다! (주석을 통해 설명했습니다!)

# v의 루트 노드 반환
def Find(v):
if(v == parent[v]):
return v
else:
p = Find(parent[v])
parent[v] = Find(parent[v])
return p
# u에는 u의 루트노드를 저장
# v에는 v의 루트노드를 저장
# 비교한다음 u에 v를 붙임 -> v의 루트노드를 x로 설정
def Union(u, v):
u = Find(u)
v = Find(v)
if(u!=v):
parent[v] = u
n,m = map(int, input().split())
parent = [i for i in range(n+1)]
for _ in range(m):
command, a, b = map(int, input().split())
if command == 0: #합집합
Union(a,b)
elif command == 1: # 같은 집합인지 확인
a_parent = Find(a)
b_parent = Find(b)
if a_parent == b_parent:
print("YES")
else:
print("NO")'CS Study > Algorithm' 카테고리의 다른 글
| 탐색 알고리즘 정리 #3 - 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.02.10 |
|---|---|
| 탐색 알고리즘 정리 #2 - 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2021.02.10 |
| 탐색 알고리즘 정리 #1 - BFS(너비 우선 탐색) , DFS(깊이 우선 탐색) (0) | 2021.02.09 |


