Shortest path between all pairs of vertices, negative edges allowed. 모든 노드 간 최단 거리를 구하는 알고리즘입니다. 플로이드-워셜 알고리즘은 다익스트라 알고리즘과는 다르게 음의 간선도 사용할 수 있습니다.
Floyd-Warshall 로직
다익스트라 알고리즘과는 다르게 플로이드-워셜 알고리즘은 모든 정점을 경유지로 만든다는데에 있습니다.
- 우선, 모든 노드 간의 최단경로를 저장해야 하기 때문에 2차원 인접 행렬을 만듭니다. 거리값은 모두 무한대로 초기화 시켜줍니다.
- 하나의 정점에서 다른 정점으로 바로 갈 수 있으면 비용을 업데이트 시켜줍니다. 이때 갈수있는 경로가 여러개라면 최소값을 저장합니다.
- 경유지를 기준으로, 어떤 두 노드가 해당 경유지를 거처갈 경우에 기존의 거리보다 더 짧다면 기존의 거리 값을 최소값으로 갱신합니다.
- 모든 정점을 경유지로 설정해 2번을 반복합니다.
이해를 돕기 위한 유튜브

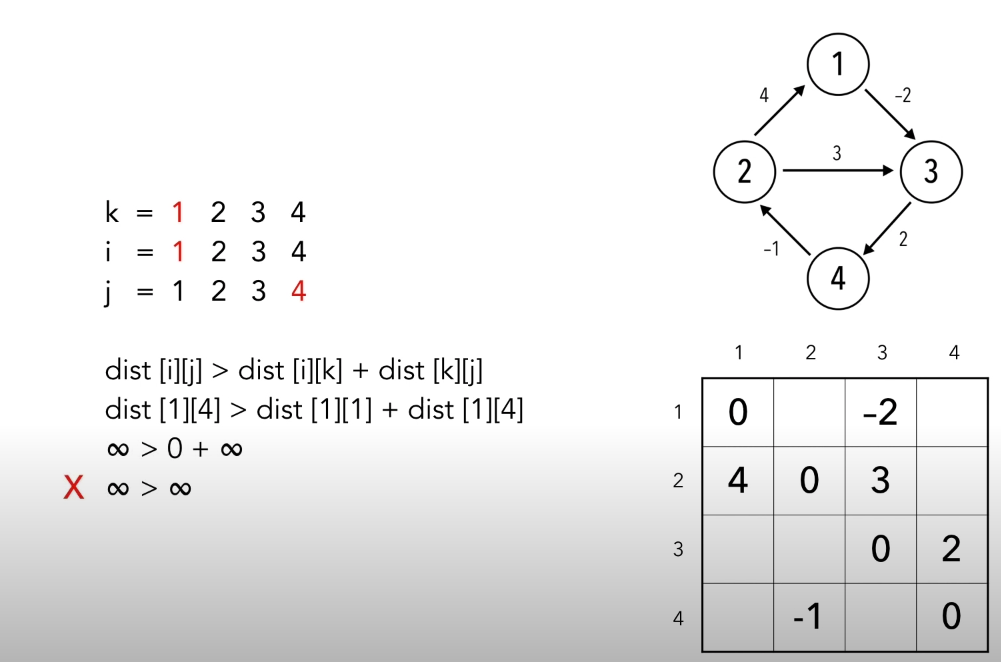
i에서 j노드로 갈때 k노드인 경유지를 거쳐가는 경우(i=> k => j)와 바로 가는 경우(i=>j)를 비교하여 더 작은 값으로 업데이트 시켜주는게 로직의 핵심입니다.
기본 문제 - [백준] 11404번 : 플로이드

Python 코드
import sys
INF = sys.maxsize
if __name__ == "__main__" :
N = int(input())
M = int(input())
#그래프 정보를 담는 인접행렬, 초기 거리는 무한대로 설정
distance = [[INF]*(N+1) for _ in range(N+1)]
#인접행렬에 u->v 로 가는 거리(cost)를 저장
for _ in range(M):
u,v,cost = map(int, input().split())
distance[u][v] = min(cost, distance[u][v])
# floyd
# k는 경유지로 모든 정점들을 경유지로 설정
for k in range(1,N+1):
for i in range(1,N+1):
for j in range(1,N+1):
if i==j:
distance[i][j] = 0
# i 노드 -> j 노드 갈때 기존 거리값과 k 노드를 거쳐간 경유지 거리값중 작은 값으로 업데이트
distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
for y in range(1,N+1):
for x in range(1,N+1):
if(distance[y][x] == INF):
print(0, end=' ')
else:
print(distance[y][x], end=' ')
print()'CS Study > Algorithm' 카테고리의 다른 글
| [그래프 이론] - Minimum Spanning Tree (최소 신장 트리) (0) | 2021.02.11 |
|---|---|
| 탐색 알고리즘 정리 #2 - 다익스트라 알고리즘(Dijkstra algorithm) (0) | 2021.02.10 |
| 탐색 알고리즘 정리 #1 - BFS(너비 우선 탐색) , DFS(깊이 우선 탐색) (0) | 2021.02.09 |


