https://www.acmicpc.net/problem/11727
11727번: 2×n 타일링 2
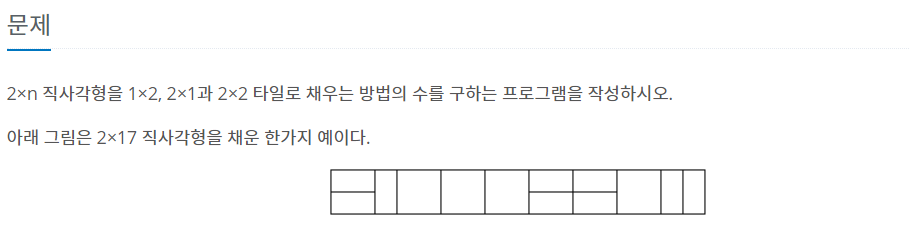
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다.
www.acmicpc.net
생각
2*n 직사각형을 1*2, 2*1, 2*2 인 세가지 타일로 채우는 경우의 수를 구하는 문제입니다.
제가 정의한 dp[n] 은 너비가 n인 직사각형을 세가지의 타일로 채우는 경우의 수입니다.
타일의 경우가 세가지가 있는데 여기서 너비가 2인 타일이 두가지가 있기 때문에 dp[n] = dp[n-1] + dp[n-2] + dp[n-2]로 생각했습니다.
2*n 직사각형을 채우는 방법은 (1)n-1 너비인 직사각형에서 너비가 1인 직사각형을 더하는 경우, (2)n-2 너비에서 1*2 타일로 채우는 경우, (3)n-2 너비에서 2*2 타일로 채우는 경우 총 세가지 방법밖에 없기 때문입니다.
첫번째 dp[n-2]의 의미는 n-2너비의 직사각형을 1*2 타일로 채우는 경우이고,
두번째 dp[n-2]의 의미는 n-2너비의 직사각형을 2*2 타일로 채우는 경우입니다.
dp[n] = dp[n-1] + dp[n-2] + dp[n-2] -> dp[n] = dp[n-1] + 2*dp[n-2] 로 써도 동일하지만 다이나믹 프로그래밍의 의미를 명확하게 하고 싶어서 풀어서 정의해줬습니다.
Java Code
package com.java.algorithm;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class BOJ_11727_2n타일링2 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] dp = new int[1001]; // 너비가 n인 직사각형 채우는 경우의 수
dp[1] = 1;
dp[2] = 3;
for (int i = 3; i <= N; i++) {
dp[i] = dp[i-1]+dp[i-2]+dp[i-2];
dp[i] = dp[i]%10007;
}
System.out.println(dp[N]);
}
}
'Algorithm' 카테고리의 다른 글
| [백준] JAVA - 14502. 연구소 (0) | 2021.03.26 |
|---|---|
| [백준] JAVA - 2636. 치즈 (0) | 2021.03.24 |
| [백준] JAVA - 11726. 2×n 타일링 (0) | 2021.03.24 |
| [백준] JAVA - 1149.RGB거리 (0) | 2021.03.23 |
| [백준] JAVA - 1463. 1로 만들기 (0) | 2021.03.23 |


